



Next: Következmények, megjegyzések
Up: Az extremális Frobenius-probléma
Previous: Az extremális problémára vonatkozó
Tartalomjegyzék
Az előbbiekhez hasonló, azonnal látható esetek kivételével vajon bővíthető-e a
felső becslések alapján a pontos  -k köre? Vannak-e olyan további
esetek, amikor a DIXMIER-féle, eddig is nagyon precíznek mutatkozó
felső becslés teljesen pontos eredményt ad?
Néhány speciális esetet részletesen kiszámolva, fokozatosan derült ki, hogy
kisebb korlátozások mellett két maradékosztályra is pontos a becslés [16].
-k köre? Vannak-e olyan további
esetek, amikor a DIXMIER-féle, eddig is nagyon precíznek mutatkozó
felső becslés teljesen pontos eredményt ad?
Néhány speciális esetet részletesen kiszámolva, fokozatosan derült ki, hogy
kisebb korlátozások mellett két maradékosztályra is pontos a becslés [16].
BIZONYÍTÁS: A 3.2.5.Tétel jelölései szerint
hiszen
 Most látjuk, hogy
Most látjuk, hogy  és
és 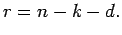 Alkalmazzuk a 3.2.5.Tétel szerinti becslést erre az esetre:
A bizonyítás befejezéséhez mutatnunk kell olyan konkrét
Alkalmazzuk a 3.2.5.Tétel szerinti becslést erre az esetre:
A bizonyítás befejezéséhez mutatnunk kell olyan konkrét
 egész számokat, amelyekkel
Vegyük külön az
egész számokat, amelyekkel
Vegyük külön az
 és
és  eseteket.
eseteket.
I. eset. Legyen először
 . Ekkor az
. Ekkor az  -et
felírhatjuk
-et
felírhatjuk
 alakban, tehát az is teljesül, hogy
alakban, tehát az is teljesül, hogy
Álljon az
 halmaz a
halmaz a  többszöröseiből
és a
többszöröseiből
és a  -től lefelé haladva abból az
-től lefelé haladva abból az  darab legnagyobb számból,
amelyek mind
darab legnagyobb számból,
amelyek mind  -gyel kongruensek modulo
-gyel kongruensek modulo  :
Látható, hogy
:
Látható, hogy
 Jelöljük
Jelöljük  -vel az
-vel az  halmaz legkisebb olyan elemét, amely nem többszöröse a
halmaz legkisebb olyan elemét, amely nem többszöröse a  -nek, azaz
Az előző fejezetben bemutatott módszer alapján tudjuk, hogy
-nek, azaz
Az előző fejezetben bemutatott módszer alapján tudjuk, hogy
 egy teljes maradékrendszert alkot
mod
egy teljes maradékrendszert alkot
mod  Így a legnagyobb szám, amely nem írható fel az
Így a legnagyobb szám, amely nem írható fel az  halmaz
elemeinek lineáris kombinációjaként:
Most felhasználjuk, hogy
halmaz
elemeinek lineáris kombinációjaként:
Most felhasználjuk, hogy
 , így
, így
II. eset. Legyen most
 . Ekkor
. Ekkor
 , illetve
, illetve
 . Ezt behelyettesítve látjuk, hogy
. Ezt behelyettesítve látjuk, hogy
 Így azt is könnyen láthatjuk, hogy
a
Így azt is könnyen láthatjuk, hogy
a  többszöröse a
többszöröse a  -nek:
-nek:
Álljon most az
 halmaz ismét a
halmaz ismét a  több-szöröseiből és a
több-szöröseiből és a  -től lefelé haladva abból az
-től lefelé haladva abból az  darab legnagyobb számból,
amelyek mind
darab legnagyobb számból,
amelyek mind  -gyel kongruensek modulo
-gyel kongruensek modulo  :
:
Látható, hogy
 Jelöljük
Jelöljük  -szel az
-szel az  halmaz legkisebb olyan elemét, amely nem többszöröse a
halmaz legkisebb olyan elemét, amely nem többszöröse a  -nek, azaz
A bizonyítást ugyanúgy folytathatjuk, mint az I. esetben.
-nek, azaz
A bizonyítást ugyanúgy folytathatjuk, mint az I. esetben.
 egy teljes maradékrendszert
alkot mod
egy teljes maradékrendszert
alkot mod Így a legnagyobb szám, amely nem írható fel az
Így a legnagyobb szám, amely nem írható fel az  halmaz
elemeinek lineáris kombinációjaként:
Felhasználjuk, hogy
halmaz
elemeinek lineáris kombinációjaként:
Felhasználjuk, hogy
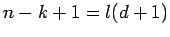 , így
, így




Next: Következmények, megjegyzések
Up: Az extremális Frobenius-probléma
Previous: Az extremális problémára vonatkozó
Tartalomjegyzék
root
2004-12-04
![]() -k köre? Vannak-e olyan további
esetek, amikor a DIXMIER-féle, eddig is nagyon precíznek mutatkozó
felső becslés teljesen pontos eredményt ad?
Néhány speciális esetet részletesen kiszámolva, fokozatosan derült ki, hogy
kisebb korlátozások mellett két maradékosztályra is pontos a becslés [16].
-k köre? Vannak-e olyan további
esetek, amikor a DIXMIER-féle, eddig is nagyon precíznek mutatkozó
felső becslés teljesen pontos eredményt ad?
Néhány speciális esetet részletesen kiszámolva, fokozatosan derült ki, hogy
kisebb korlátozások mellett két maradékosztályra is pontos a becslés [16].
![]() . Ekkor az
. Ekkor az ![]() -et
felírhatjuk
-et
felírhatjuk
![]() alakban, tehát az is teljesül, hogy
alakban, tehát az is teljesül, hogy
![]() . Ekkor
. Ekkor
![]() , illetve
, illetve
![]() . Ezt behelyettesítve látjuk, hogy
. Ezt behelyettesítve látjuk, hogy
![]() Így azt is könnyen láthatjuk, hogy
a
Így azt is könnyen láthatjuk, hogy
a ![]() többszöröse a
többszöröse a ![]() -nek:
-nek:
![]() halmaz ismét a
halmaz ismét a ![]() több-szöröseiből és a
több-szöröseiből és a ![]() -től lefelé haladva abból az
-től lefelé haladva abból az ![]() darab legnagyobb számból,
amelyek mind
darab legnagyobb számból,
amelyek mind ![]() -gyel kongruensek modulo
-gyel kongruensek modulo ![]() :
: