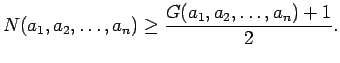Next: Ízelítő az extremális Frobenius-problémából
Up: A pénzváltási probléma az
Previous: Keressük a legnagyobb nem
Tartalomjegyzék
SYLVESTER [30] 1884-ben megjelent problémái között szerepelt
az előző fejezet 3. feladatához kapcsolódó kérdés
felvetése és megoldása.
FELADAT 8 Legyen két különböző címletű
érménk és ezekből elegendően sok. Határozzuk meg
azoknak a pozitív egészeknek a számát, amelyek nem ,,fizethetők
ki'' ezen kétféle érme segítségével maradék nélkül.
A korábbi jelölésekkel
 pontos értékét
keressük. A meg-oldáshoz felhasználjuk, hogy
pontos értékét
keressük. A meg-oldáshoz felhasználjuk, hogy
minden nullától különböző maradékot tartalmazó
maradékrendszert alkot mod  Az egyes maradékosztályokban ezek a felsorolt elemek lesznek a
legkisebb felírhatók, továbbá tudjuk, hogy ezek a számok
éppen az
Az egyes maradékosztályokban ezek a felsorolt elemek lesznek a
legkisebb felírhatók, továbbá tudjuk, hogy ezek a számok
éppen az
 egy permutációjának
elemeivel lesznek rendre kongruensek mod
egy permutációjának
elemeivel lesznek rendre kongruensek mod  Legyen ez a
permutáció
Legyen ez a
permutáció
 Ekkor a
Ekkor a
 maradékosztályban a nem felírható elemek száma pontosan
Ezeket a számokat összegezve az összes nemnulla
maradékosztályra megkapjuk a nem felírható elemeket:
maradékosztályban a nem felírható elemek száma pontosan
Ezeket a számokat összegezve az összes nemnulla
maradékosztályra megkapjuk a nem felírható elemeket:
SELMER [28] az előbbi módszert általánosan alkalmazta.
Legyen  egy teljes maradékrendszer mod
egy teljes maradékrendszer mod  Minden
Minden
 -hoz van olyan
-hoz van olyan
 , amely felírható
, amely felírható
 alakban és a legkisebb.
Ezekkel a jelölésekkel
alakban és a legkisebb.
Ezekkel a jelölésekkel
Alkalmazzuk ezt az interpretációt további feladatokban is.
Először az egyes osztályokba tartozó legkisebb  maradékokat kell megadnunk.
maradékokat kell megadnunk.
 teljes
maradékrendszert alkot
teljes
maradékrendszert alkot
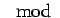
 . A célunk az, hogy
a legnagyobb maradékot is a legkevesebb
. A célunk az, hogy
a legnagyobb maradékot is a legkevesebb  felhasználásával állítsuk elő.
Ennek érdekében az
felhasználásával állítsuk elő.
Ennek érdekében az  -et, amelynek maradéka
-et, amelynek maradéka  a
lehetséges legnagyobb szorzóval vesszük:
a
lehetséges legnagyobb szorzóval vesszük:
Ez alapján
Ennek megfelelően
 maradéka megegyezik
maradéka megegyezik  maradékával mod
maradékával mod  Az
Az  rendszer táblázatba
rendezhető:
Az utolsó sor csak akkor szükséges, ha
rendszer táblázatba
rendezhető:
Az utolsó sor csak akkor szükséges, ha 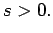
A táblázatban a  többszöröseinek összege az eredeti
felírás alapján:
Az
többszöröseinek összege az eredeti
felírás alapján:
Az  többszöröseinek összegére:
többszöröseinek összegére:
Ezzel az állítást igazoltuk, sőt a táblázatból
kiolvasható, hogy a legnagyobb nem felírható szám 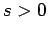 esetén
esetén
Amennyiben  , a legnagyobb nem felírható számra azt kapjuk, hogy
A két formula írható azonos alakban, mivel
, a legnagyobb nem felírható számra azt kapjuk, hogy
A két formula írható azonos alakban, mivel 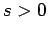 -ra
Ezzel a 6. feladat állítását is beláttuk.
-ra
Ezzel a 6. feladat állítását is beláttuk.

Következő, kevésbé ismert eredményünk az 1. feladathoz
kapcsolódik.
FELADAT 10 Legyenek  páronként relatív
prím pozitív egész számok. Mutassuk meg, hogy azoknak a
számoknak a száma, amelyek nem írhatók fel
páronként relatív
prím pozitív egész számok. Mutassuk meg, hogy azoknak a
számoknak a száma, amelyek nem írhatók fel
 alakban, ahol
alakban, ahol 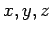 nemnegatív egész számok,
nemnegatív egész számok,
Ebben az esetben is áttekinthetően megadhatjuk mod  az egyes maradékosztályokban a
az egyes maradékosztályokban a  és
és 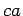 segítségével
felírható legkisebb elemeket:
segítségével
felírható legkisebb elemeket:
A táblázatban pontosan  darab szám szerepel. Elegendő
tehát belátnunk, hogy páronként inkongruensek mod
darab szám szerepel. Elegendő
tehát belátnunk, hogy páronként inkongruensek mod  Ellenkező esetben
Ez pontosan azt jelenti, hogy
osztható
Ellenkező esetben
Ez pontosan azt jelenti, hogy
osztható  -vel.
-vel.
Azonnal látható, hogy az oszthatósági tulajdonságok miatt
 osztható lesz
osztható lesz  -val,
-val,  pedig
pedig  -vel.
Mivel
-vel.
Mivel
 és
és
 , az
oszthatóság csak
, az
oszthatóság csak 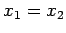 , valamint
, valamint  esetében
lehet igaz.
esetében
lehet igaz.
Adjuk most össze a reprezentánsokat:
Alkalmazzuk a Selmer-féle formulát:
A nem felírható számok meghatározása során tulajdonképpen
egy harmadik megoldást nyertünk az 1. feladatra, mivel
láthatóan a legnagyobb 
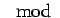
 pontosan
pontosan
 lesz. Innen rögtön felírhatjuk, hogy
lesz. Innen rögtön felírhatjuk, hogy
Az
 -et a
-et a
 -hez viszonyítva érdekes
-hez viszonyítva érdekes
megfigyelést tehetünk. Összehasonlítva az 1. és 10. feladat, továbbá a 3. és
8. feladat formuláit, azt látjuk, hogy
Fontos határeseteit kaptuk NIJENHUIS és WILF [22] tételének, akik
annak az egyszerű ténynek a felismerése alapján, hogy
tetszőleges olyan  és
és  pozitív egészek közül,
amelyek összege
pozitív egészek közül,
amelyek összege
 , legfeljebb az egyik
lehet felírható az
, legfeljebb az egyik
lehet felírható az
 segítségével,
kapták, hogy
segítségével,
kapták, hogy
Felső becslésként azonnal adódik, hogy
Ez a becslés nem is javítható, hiszen
választással pontosan





Next: Ízelítő az extremális Frobenius-problémából
Up: A pénzváltási probléma az
Previous: Keressük a legnagyobb nem
Tartalomjegyzék
root
2004-12-04
![]() pontos értékét
keressük. A meg-oldáshoz felhasználjuk, hogy
pontos értékét
keressük. A meg-oldáshoz felhasználjuk, hogy




![]() egy teljes maradékrendszer mod
egy teljes maradékrendszer mod ![]() Minden
Minden
![]() -hoz van olyan
-hoz van olyan
![]() , amely felírható
, amely felírható
![]() alakban és a legkisebb.
Ezekkel a jelölésekkel
alakban és a legkisebb.
Ezekkel a jelölésekkel


![]() maradékokat kell megadnunk.
maradékokat kell megadnunk.
![]() teljes
maradékrendszert alkot
teljes
maradékrendszert alkot
![]()
![]() . A célunk az, hogy
a legnagyobb maradékot is a legkevesebb
. A célunk az, hogy
a legnagyobb maradékot is a legkevesebb ![]() felhasználásával állítsuk elő.
Ennek érdekében az
felhasználásával állítsuk elő.
Ennek érdekében az ![]() -et, amelynek maradéka
-et, amelynek maradéka ![]() a
lehetséges legnagyobb szorzóval vesszük:
a
lehetséges legnagyobb szorzóval vesszük:






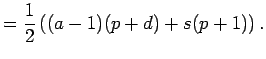
![]() esetén
esetén
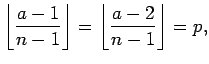
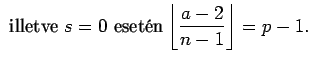

![]() az egyes maradékosztályokban a
az egyes maradékosztályokban a ![]() és
és ![]() segítségével
felírható legkisebb elemeket:
segítségével
felírható legkisebb elemeket:

![]() osztható lesz
osztható lesz ![]() -val,
-val, ![]() pedig
pedig ![]() -vel.
Mivel
-vel.
Mivel
![]() és
és
![]() , az
oszthatóság csak
, az
oszthatóság csak ![]() , valamint
, valamint ![]() esetében
lehet igaz.
esetében
lehet igaz.

![$\displaystyle =\frac{abc}{2}\left[b(a-1)+a(b-1)\right].$](img177.png)
![$\displaystyle N(ab, bc, ca)=\frac{1}{ab}\cdot \frac{abc}{2}\left[a(b-1)+b(a-1)\right]-
\frac {ab-1}{2}=
$](img178.png)

![]()
![]()
![]() pontosan
pontosan
![]() lesz. Innen rögtön felírhatjuk, hogy
lesz. Innen rögtön felírhatjuk, hogy
![]() -et a
-et a
![]() -hez viszonyítva érdekes
-hez viszonyítva érdekes