



Next: Összegzések elemi módszerrel
Up: A nem felírható számok
Previous: Generátorfüggvény és a nem
Tartalomjegyzék
Ö. J. RÖDSETH [27] erős analitikus eszközökkel
BROWN és SHIUE előbb bizonyított 5.2.1. Tételét
jelentősen általánosította.
Az  és
és  relatív prím pozitív egészek esetében jelölje most is
NR
relatív prím pozitív egészek esetében jelölje most is
NR azoknak a nemnegatív egészeknek a halmazát, amelyek nem fejezhetők ki
azoknak a nemnegatív egészeknek a halmazát, amelyek nem fejezhetők ki
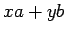 alakban, ahol
alakban, ahol  és
és  nemnegatív egészek. Legyen
nemnegatív egészek. Legyen  ezen nemnegatív egészek
ezen nemnegatív egészek  -edik hatványainak összege:
-edik hatványainak összege:
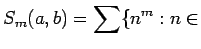
NR

A hatványösszegek felírhatók zárt alakban:
TÉTEL 5.3.1
Tetszőleges  pozitív egészre
ahol a
pozitív egészre
ahol a  -k az ún. Bernoulli-féle számok.
-k az ún. Bernoulli-féle számok.
A szakirodalomban több helyen megtalálható (pl. [10])
Bernoulli-féle számok egy hatványsor együtthatói:

A tételt nem bizonyítjuk, de néhány  -re az összeget pontosan
kiszámítjuk.
-re az összeget pontosan
kiszámítjuk.
Az  esetben a nem felírható számok számát kapjuk
(ld. 2. fejezet 8. feladat), azaz
esetben a nem felírható számok számát kapjuk
(ld. 2. fejezet 8. feladat), azaz
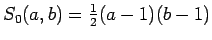 .
Alkalmazzuk ezt az általános eredményt először
.
Alkalmazzuk ezt az általános eredményt először  kiszámítására:
kiszámítására:
BIZONYÍTÁS: Legyen  , ekkor a formula átírható:
, ekkor a formula átírható:
Most következhet a nem felírható számok négyzetösszegének meghatározása.
BIZONYÍTÁS: Legyen  , ekkor a formula átírható:
Kihasználva, hogy
, ekkor a formula átírható:
Kihasználva, hogy  , néhány tagot eleve elhagyhattunk. Beírva a binomiális együthatók értékét és
egyszerűbb alakra hozva:
Az előző két levezetésből látható, hogy az általános formulából rövidebb
számolással
, néhány tagot eleve elhagyhattunk. Beírva a binomiális együthatók értékét és
egyszerűbb alakra hozva:
Az előző két levezetésből látható, hogy az általános formulából rövidebb
számolással  esetén akármelyik hatványösszege meghatározható a
nem felírható számoknak.
A későbbi összehasonlíthatóság érdekében számoljuk ki még az
esetén akármelyik hatványösszege meghatározható a
nem felírható számoknak.
A későbbi összehasonlíthatóság érdekében számoljuk ki még az  -t is.
-t is.
BIZONYÍTÁS: Legyen  , ekkor a formula átírható:
A kifejtésnél a
, ekkor a formula átírható:
A kifejtésnél a 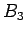 -at tartalmazó tagokat nem írjuk le.
Beírva az egyes konkrét értékeket és rendezve:
adódik. Ez további azonos átalakításokkal rövidebb alakra hozható:
Az
-at tartalmazó tagokat nem írjuk le.
Beírva az egyes konkrét értékeket és rendezve:
adódik. Ez további azonos átalakításokkal rövidebb alakra hozható:
Az
 tényező tetszőleges
tényező tetszőleges  -re kiemelhető a kifejezésből.
Páros
-re kiemelhető a kifejezésből.
Páros  esetében további szimmetriát jelent, hogy az
esetében további szimmetriát jelent, hogy az  -nél nagyobb
páratlan indexű Bernoulli-számok mindegyike 0, így azokban az ösz-szegekben nincs konstans,
kiemelhető
-nél nagyobb
páratlan indexű Bernoulli-számok mindegyike 0, így azokban az ösz-szegekben nincs konstans,
kiemelhető  is.
is.




Next: Összegzések elemi módszerrel
Up: A nem felírható számok
Previous: Generátorfüggvény és a nem
Tartalomjegyzék
root
2004-12-04
![]() és
és ![]() relatív prím pozitív egészek esetében jelölje most is
NR
relatív prím pozitív egészek esetében jelölje most is
NR![]() azoknak a nemnegatív egészeknek a halmazát, amelyek nem fejezhetők ki
azoknak a nemnegatív egészeknek a halmazát, amelyek nem fejezhetők ki
![]() alakban, ahol
alakban, ahol ![]() és
és ![]() nemnegatív egészek. Legyen
nemnegatív egészek. Legyen ![]() ezen nemnegatív egészek
ezen nemnegatív egészek ![]() -edik hatványainak összege:
-edik hatványainak összege:

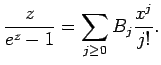
![]() -re az összeget pontosan
kiszámítjuk.
-re az összeget pontosan
kiszámítjuk.
![]() esetben a nem felírható számok számát kapjuk
(ld. 2. fejezet 8. feladat), azaz
esetben a nem felírható számok számát kapjuk
(ld. 2. fejezet 8. feladat), azaz
![]() .
Alkalmazzuk ezt az általános eredményt először
.
Alkalmazzuk ezt az általános eredményt először ![]() kiszámítására:
kiszámítására:
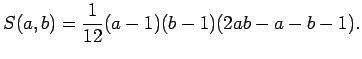
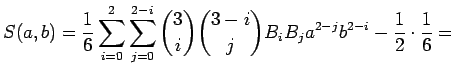
![$\displaystyle =\frac{1}{6}\binom{3}{0}B_0b^2\left[\binom{3}{0}B_0a^2+\binom{3}{1}B_1a+\binom{3}{2}B_2\right]+
$](img589.png)
![$\displaystyle +\frac{1}{6}\binom{3}{1}B_1b\left[\binom{2}{0}B_0a^2+\binom{2}{1}...
...ight]
+\frac{1}{6}\binom{3}{2}B_2\left[\binom{1}{0}B_0a^2\right]-\frac{1}{12}=
$](img590.png)


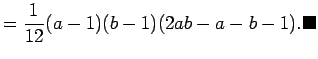


![$\displaystyle =\frac{1}{12}\binom{4}{0}B_0b^3\left[\binom{4}{0}B_0a^3+\binom{4}{1}B_1a^2+\binom{4}{2}B_2a+\binom{4}{3}B_3\right]+
$](img596.png)
![$\displaystyle +\frac{1}{12}\binom{4}{1}B_1b^2\left[\binom{3}{0}B_0a^3+\binom{3}{1}B_1a^2+\binom{3}{2}B_2a\right]+
$](img597.png)
![$\displaystyle +\frac{1}{12}\binom{4}{2}B_2b\left[\binom{2}{0}B_0a^3+\binom{2}{1}B_1a^2\right].
$](img598.png)


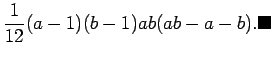


![$\displaystyle =\frac{1}{20}\binom{5}{0}B_0b^4\left[\binom{5}{0}B_0a^4+\binom{5}{1}B_1a^3+\binom{5}{2}B_2a^2+\binom{5}{4}B_4\right]+
$](img608.png)
![$\displaystyle +\frac{1}{20}\binom{5}{1}B_1b^3\left[\binom{4}{0}B_0a^4+\binom{4}{1}B_1a^3+\binom{4}{2}B_2a^2\right]+
$](img609.png)
![$\displaystyle +\frac{1}{20}\binom{5}{2}B_2b^2\left[\binom{3}{0}B_0a^4+\binom{3}{1}B_1a^3+\binom{3}{2}B_2a^2\right]+
$](img610.png)


